Ομοιότητα και γραμμική συνάρτηση

Μελέτη περίπτωσης

 Εισαγωγή

Δύο από τις σημαντικότερες έννοιες των σχολικών μαθηματικών είναι η γραμμικότητα ([1], [2], [3], [4], [5], [6]) και η ομοιότητα ([1], [2], [3], [4], [5], [6]). Δύο διαφορετικές μαθηματικές έννοιες που συνδέονται πολύ στενά, μέσω του λόγου μεταβολής των διαστάσεων των όμοιων σχημάτων που είναι και κλίσης της ευθείας.

   Η γραμμικότητα διαπερνά το σύνολο του οικοδομήματος των σχολικών μαθηματικών. Από τη μέτρηση των μεγεθών, την έννοια των αναλόγων ποσών και την αναλογία  μέχρι τη γραμμική άλγεβρα, τη χρήση των γραμμικών μοντέλων στο απειροστικό λογισμό, τις πιθανότητες  και τη στατιστική. Σε κάθε περίπτωση η γραμμικότητα ικανοποιεί τις δύο συνθήκες των γραμμικών συναρτήσεων  f(x+y)=f(x)+f(y) και f(kx)=kf(x).
   Η ομοιότητα από την άλλη, στα σχολικά μας μαθηματικά, είναι συνδεδεμένη πιο πολύ με την γεωμετρία, με την σύγκριση των επίπεδων και στερεών σχημάτων καθώς και με την διατήρηση των γωνιών και του λόγου των πλευρών τους, και λιγότερο με την Άλγεβρα (τον λόγο και την αναλογία) με αποτέλεσμα οι μαθητές να τείνουν να αναπτύσσουν προσθετικές στρατηγικές για να προκαλέσουν μεγέθυνση ή σμίκρυνση ενός σχήματος. Σε αυτό αναφέρεται ο Guy Brousseau στο βιβλίο "Theory of didactical situations in mathematics"([1]).

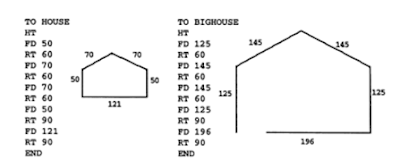
Το πρόβλημα:  Να κατασκευαστεί μια μεγέθυνση του διπλανού μοντέλου όπου το τμήμα μήκους 4 cm  να είναι 7cm στο νέο μοντέλο.  Η προσθετική διαδικασία:  Σχεδόν όλοι οι μαθητές σκέφτηκαν να προσθέσουν 3 στο 4 και σε κάθε άλλο μήκος.   Η γνωστική σύγκρουση: Στο νέο μοντέλο τα κομμάτια δεν είναι συμβατά.

   Ένα αντίστοιχο θέμα παρουσιάζεται στο βιβλίο των Noss R. και Hoyles C. "Windows of mathematical meanings: learning cultures and computers [1].

Το πρόβλημα: Στους μαθητές δόθηκε η διαδικασία αριστερά και τους ζητήθηκε να την τροποποιήσουν ώστε να παραχθεί μια μεγέθυνση του σπιτιού.  Η διαδικασία: Η προσθετική διαδικασία (FD 50 -> FD 125, ...) που επέλεξαν δεν έδωσε μια μεγέθυνση του σπιτιού στα δεξιά. Η γνωστική σύγκρουση:  Τα πειράματα βοήθησαν να κλείσει η τρύπα στο μεγάλο σπίτι (FD1 = FD * 125/50) και να γίνει άρση της προσθετικής αντίληψης για την σμίκρυνση -  μεγέθυνση.

(H χελωνόσφαιρα είναι ένα κατάλληλο περιβάλλο για να πειραματιστεί κάποιος με το σπίτι)

   Υιοθετώντας την πρόταση του G. Vergnaud για το εννοιολογικό πεδίο   ([1], [2], [3]), δύο έννοιες - γραμμικότητα και ομοιότητα - θα μπορούσαμε να τις εντάξουμε ανήκουν στο ίδιο μαζί με την πολλαπλασιαστική δομή.
   Στο σχολικό πρόγραμμα οι δύο έννοιες δύσκολα συνδέονται καθώς η μία είναι αντικείμενο της γεωμετρίας και η άλλη της Άλγεβρας που συχνά διδάσκονται στην ίδια τάξη από διαφορετικούς καθηγητές.
   Το συγκεκριμένο άρθρο είναι μια πρόταση για μια συνειδητή σύνδεση των δύο εννοιών και μια μερική αποκατάσταση της έλλειψης της συνεκτικότητας μεταξύ των  μαθηματικών αντικειμένων.
   

Η δραστηριότητα

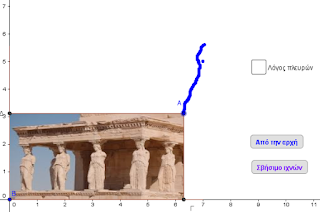
Στην παρακάτω εφαρμογή ο χρήστης - μαθητής καλείται να μετακινεί το σημείο Α για να μεταβάλλει τις διαστάσεις της εικόνας, έτσι ώστε να προκαλεί σμίκρυνση ή μεγέθυνση. Καλείται επίσης να πληκτρολογήσει την εξίσωση της διαδρομής - τύπου y=ax - και να επιβεβαιώσει το συμπέρασμά του.
   Δηλαδή, ο χρήστης - μαθητής καλείται από τη ομοιότητα ενός γεωμετρικού σχήματος να οδηγηθεί στην συνάρτηση f(x)=ax. Με την διαδικασία "Έλεγχος" μπορεί  να δει την αντίστροφη διαδικασία. Δηλαδή, να κινεί το σημείο Θ στην ευθεία y=ax και να παρατηρεί την επίδρασή που ασκεί στο σχήμα (εικόνα).

 

Ανάλυση την δραστηριότητας

Το σημείο Α έχει την ιδιότητα να κινείται και προς κάθε κατεύθυνση στο επίπεδο (οριζόντια, κατακόρυφα αλλά και διαγώνια).
   Ο χρήστης πρέπει να βρει την κατάλληλη διαδρομή του σημείου Α ώστε να προκαλείται σμίκρυνση ή μεγέθυνση της εικόνας και όχι στρέβλωση, όπως στις παρακάτω εικόνες.


   Τα πειράματα: Η εύρεση της κατάλληλης διαδρομής αρχικά αναμένεται να προσδιοριστεί με τη βοήθεια διαισθητικών στοιχείων που θα προκύψουν από τις δοκιμές. Δηλαδή ο χρήστης - μαθητής θα χρειαστεί να κάνει δοκιμές μέχρι να κατανοήσει (1) πότε πραγματοποιείται σμίκρυνση ή μεγέθυνση και (2) τι είδους σχήμα είναι η διαδρομή.
   Η διερεύνηση: Αλλά χωρίς γνώση των ιδιοτήτων της διαδρομής, είναι δύσκολο αυτή να προσδιοριστεί με ακρίβεια. Για τον προσδιορισμό των ιδιοτήτων θα βοηθήσει ο λόγος των διαστάσεων της εικόνας κατά την σμίκρυνση ή μεγέθυνση, σε σχέση με την αρχική. Σε αυτό θα βοηθήσει ο λόγος των δύο διαστάσεων και η απαίτηση να διατηρείται κατά τον μετασχηματισμό της εικόνας. Δηλαδή η ζητούμενη διαδρομή είναι ο γεωμετρικός τόπος των θέσεων του Α στις οποίες η εικόνα είναι όμοια με την αρχική. Η διαδρομή προσδιορίζεται από τον λόγο των δύο διαστάσεων της εικόνας λ= 5,56/7 = 0,79 και της γραφικής παράστασης της εξίσωσης y=0.79x.
   Ο έλεγχος:  Με του κουτί "Έλεγχος" εμφανίζεται η ευθεία y=0.79x καθώς και το σημείο Θ σε αυτή. Η μετακίνηση του Θ προκαλεί σμίκρυνση ή μεγέθυνση της εικόνας, η οποία φυσικά βρίσκεται σε άλλη θέση, για να μην συνδεθεί η αρχή της εικόνας με την ευθεία y=0.79x.

Η διδακτική πρόταση

Πέρα από τους στόχους της διδασκαλίας για κάθε μια έννοια ξεχωριστά, η διδασκαλία πρέπει να στοχεύει και στη σύνδεση των δύο εννοιών κατά κάποιο τρόπο.
   Η διασύνδεση μπορεί να γίνει είτε εντός των μαθηματικών (γεωμετρία + συναρτήσεις) είτε εκτός των Μαθηματικών (π.χ. Φυσική: Το διάστημα που διανύει ένα κινητό που κάνει ευθύγραμμη ομαλή κίνηση ως προς τον χρόνο ή η ταχύτητα στη ευθύγραμμη ομαλά επιταχυνόμενη κίνηση σε σχέση με τον χρόνο).
   Ένας άλλος τρόπος διασύνδεσης των δύο εννοιών είναι η ανάδειξη των κοινών στοιχείων των δομών τους. Στο παρακάτω εννοιολογικό χάρτη, ο λόγος και η αναλογία είναι κοινά στοιχεία των δύο εννοιών και άρα μπορούν να συντελέσουν στην διασύνδεση των δύο εννοιών. Πιο συγκεκριμένα τα νοήματα που αναπτύσσει κάποιος για τον λόγο όταν μελετά την ομοιότητα και τα νοήματα που αναπτύσσει όταν μελετά την ευθεία y=ax μπορούν να ειδωθούν ως εκφράσεις του ίδιου αντικειμένου, αρκεί να μπορεί να περνά με σχετική ευκολία από το ένα νόημα στο άλλο.

Ένας εννοιολογικός χάρτης για τη σύνδεση των δύο εννοιών.

Παράδειγμα:
Το παρακάτω γράφημα αντιστοιχεί στη γραμμική συνάρτηση y=0.8x.

• Ποιά δραστηριότητα μπορεί να βοηθήσει τους μαθητές να συνδέσουν την γραμμική συνάρτηση με την ομοιότητα των τριγώνων;
• Ποια διδακτική προσέγγιση είναι η καταλληλότερη για να ενισχύσει την σύνδεση των δύο εννοιών;

Ένας εκπαιδευτικός σκέφτεται να σχεδιάσει ένα σημείο στη γράφημα και να αξιοποιήσει τις συντεταγμένες του καθώς και την κλίση για να δημιουργήσει ένα τρίγωνο το οποίο θα υφίσταται σμίκρυνση ή μεγέθυνση μεγεθύνεται ανάλογα με την κίνηση του σημείου.

• Πώς θα σχεδιάσει και αναπτύξει την εφαρμογή σε ένα λογισμικό δυναμικής γεωμετρίας;
• Ποιά ερωτήματα πρέπει να θέσει στους μαθητές του;

Το διδακτικό πρόβλημα της εξάρτησης από την γραμμική συνάρτηση και την αναλογική σχέση

Υπάρχουν πολλές αναφορές που δηλώνουν την ισχυρή εξάρτηση των μαθητών από την γραμμικότητα.  

• de Bock, D., van Dooren, W., Janssens, D., Verschaffel, L. (2007). A Widespread Phenomenon in "The Illusion of Linearity. From Analysis to Improvement". Springer Science+Business Media, LL..
• Leinhardt, G., Zaslavsky, O., & Stein, M. K. (1990). Functions, graphs, and graphing: Tasks, learning, and teaching. Review of  Educational Research,60, 1–64.
• Markovits, Z., Eylon, B.-S., & Bruckheimer, M. (1986). Functions today and yesterday. For the Learning of Mathematics, 6(2), 18–24, 28.
• De Bock, D., Verschaffel, L., & Janssens, D. (1998). The predominance of the linear model in secondary school students’ solutions of word problems involving length and area of similar plane figures. Educational Studies in Mathematics, 35, 65–83. 

   Δηλαδή οι μαθητές έχουν την τάση να χρησιμοποιούν την αναλογική σκέψη και την γραμμικότητα άκριτα, είτε στη λύση προβλημάτων είτε στην εύρεση μοτίβων κατά την μεταβολή ποσοτήτων. Ιδιαίτερα, όταν τους ζητείται να σχεδιάσουν το γράφημα μιας σχέσης, τείνουν να σχεδιάσουν μια ευθεία που να διέρχεται από την αρχή των αξόνων.
   Υπάρχουν δύο κριτήρια για τον έλεγχο της γραμμικότητας μιας συνάρτησης y=f(x). Το ένα αφορά το γράφημά της. Για να είναι γραμμική η σχέση πρέπει να είναι ευθεία και διέρχεται από την αρχή των αξόνων. Το άλλο αφορά τους δύο νόμους της γραμμικότητας

f(a+b) = f(a) + f(b) και f(ax)=af(x)

Για να είναι μια σχέση γραμμική θα πρέπει τα αριθμητικά δεδομένα να ικανοποιούν και τις δύο εξισώσεις. Το τελευταίο είναι ιδιαίτερα χρήσιμο στο μικροεπίπεδο της σχέσης (όταν τα δεδομένα αφορούν ένα πολύ μικρό εύρος των μεταβολών). Για παράδειγμα, όταν ζητείται από τους μαθητές να παρεμβάλουν ένα νέο σημείο ανάμεσα σε δύο σημεία μιας σχέσης, συνήθως χρησιμοποιούν τον αριθμητικό μέσο ώστε να τους εξασφαλίσει την γραμμικότητα. Πιο χαρακτηριστικό παράδειγμα είναι η γραμμικότητα ή όχι της συνάρτησης g(x)=ax+b. Καθώς η γραφική της παράσταση είναι ευθεία συχνά συμπεραίνουν για την γραμμικότητα της σχέσης, παρόλο που δεν διέρχεται από την αρχή των αξόνων.
   Ο έλεγχος λοιπόν της γραμμικότητα με το ένα ή το άλλο κριτήριο  είναι χρήσιμος για την γραμμικότητα και την αναλογική σκέψη. Ένας διδακτικός σχεδιασμός πρέπει να λάβει υπόψη του την συνήθως υπερβολική εξάρτηση των μαθητών από την γραμμικότητα και να εντάξει σε αυτόν κριτήρια αναλογικότητας αλλά και διαδικασίες διασυνδεσιμότητας της έννοιας, όπως αυτή που προτείνεται εδώ.  

Κ. Γαβρίλης